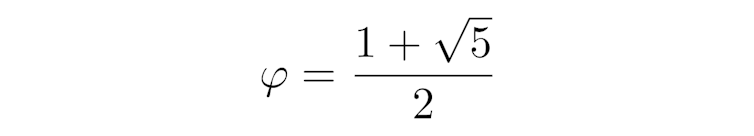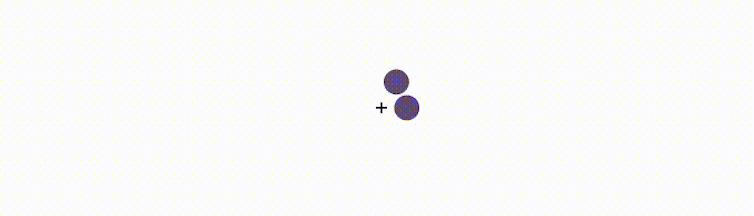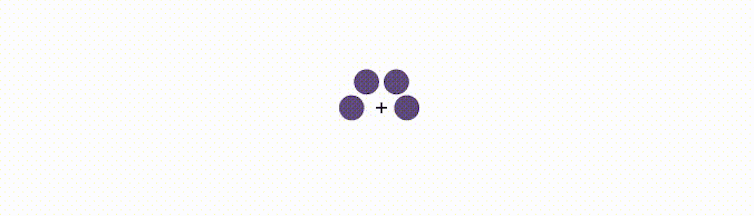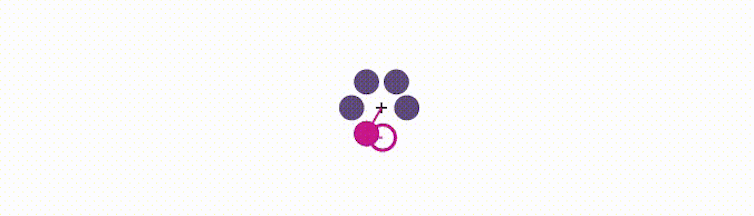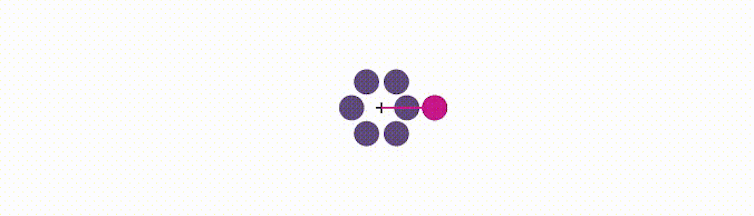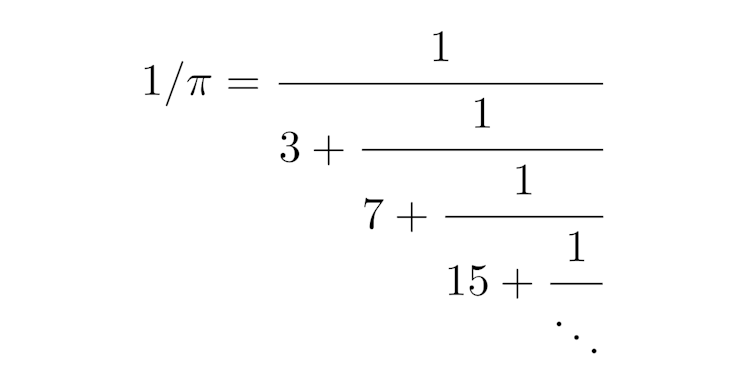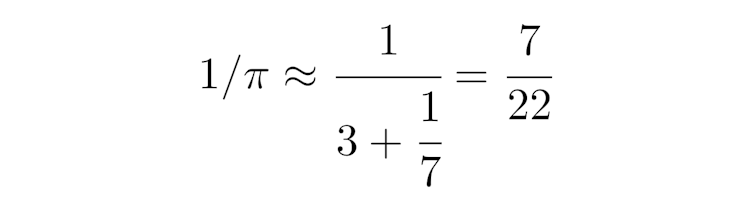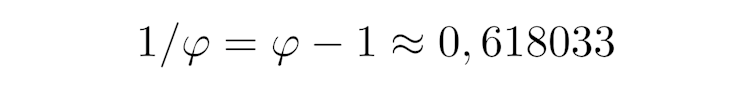1, 1, 2, 3, 5, 8, 13, 21, 34…

Les lecteurs les plus perspicaces auront reconnu le début de la célèbre suite de Fibonacci, dans laquelle chaque nouveau terme est obtenu comme la somme des deux termes précédents, et connue pour ses liens avec le mythique nombre d’or

valeur exacte du nombre d’or.

Au début du XIII^e siècle, lorsque Leonardo Fibonacci introduit cette suite dans son traité « Liber Abaci » pour modéliser de manière très simplifiée l’évolution d’une population de lapins immortels, il ne se doute pas de l’importance qu’elle acquerra en mathématiques, au point qu’une revue scientifique lui sera entièrement consacrée quelques siècles plus tard (The Fibonacci Quaterly, créée en 1963).

Il n’avait probablement pas réalisé non plus que les termes de cette suite se retrouvent fréquemment dans la nature, non pas dans l’étude de la démographie des lapins… mais en botanique !

Sur les cônes de pin, les ananas, ou les fleurs de la famille des tournesols, on observe des motifs en forme de spirales, qui s’organisent en deux réseaux qui se croisent. Si la curiosité nous pousse à compter les spirales de ces réseaux, on obtient très souvent deux nombres consécutifs de la suite de Fibonacci. Par exemple sur un cône de pin on compte en général 8 spirales dans un sens et 13 spirales dans l’autre sens. Au cœur d’une marguerite ou d’un aster, les minuscules fleurs disposées sur le capitule (les fleurons) forment deux familles de 13 et 21 spirales, voire 21 et 34.

Sur des fleurs plus grosses comme des tournesols, on trouve les paires (34,55) ou (55,89), et éventuellement plus.

Aster.

Cône de pin.

Variété de marguerite.

Il semble difficile de croire à une simple coïncidence : la régularité de ce phénomène semble plutôt révéler la mise en œuvre de principes mathématiques dans les mécanismes complexes de la croissance des plantes.

Ce sont des travaux de phyllotaxie, la science qui étudie les arrangements (géométriques) des feuilles, fleurs ou pétales des plantes, qui ont mis en évidence ces principes dès le XIXᵉ siècle.

Les mathématiciens et informaticiens se sont ensuite penchés sur la question, et ont travaillé sur des modèles permettant de décrire de manière simplifiée les mécanismes de formation des végétaux.

Un modèle pour les fleurs de tournesol

Nous avons réalisé une application en ligne qui montre le fonctionnement d’un de ces modèles, basé sur les travaux de Helmut Vogel.

Le même type de modèle est utilisé dans cette excellente vidéo (en anglais) de Numberphile, dont nous nous sommes également inspirés pour les explications qui vont suivre.

Ce modèle repose sur un principe général : les organes d’une plante comme les feuilles, les pétales, ou ici les fleurons, poussent les uns à la suite des autres en formant à chaque fois un angle fixé avec le précédent. Cet angle s’appelle l’angle de divergence, et on l’exprime en général comme une proportion d’un tour complet.

Ainsi, un angle de divergence qui vaut 1/6 signifie que l’on tourne d’un sixième de tour autour du centre du capitule pour placer le fleuron suivant. Si la position du nouveau fleuron après cette rotation vient à se superposer avec un fleuron déjà existant, on augmente la distance au centre du capitule de façon à s’écarter suffisamment de l’ancien fleuron.

début de la construction pour un angle de divergence valant 1/6.

Dans ce modèle, le processus se termine lorsque l’on arrive au bord d’un disque dont la taille est fixée à l’avance. Quelle figure obtient-on alors ? L’allure de celle-ci dépend fortement de la valeur de l’angle de divergence. Voyons d’abord le résultat pour des valeurs simples.

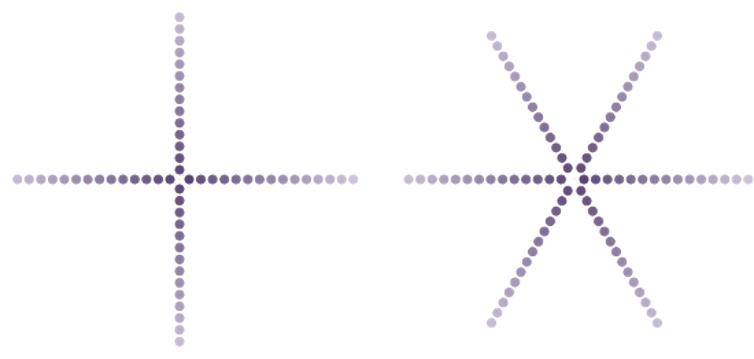
  simulations pour ¼ et 1/6.

simulation pour 11/23.

Des branches dans les fleurs

Quand on tourne d’un quart de tour (première image), il se forme 4 branches rectilignes, ce qui s’explique facilement : si on répète 4 fois cette opération, on revient dans la direction de départ. De même, un sixième de tour donne 6 branches (seconde image). Lorsque l’angle de divergence vaut 11/23 (troisième image), 23 itérations de la rotation correspondent à 11 tours complets, donc aboutissent aussi à la direction de départ : on obtient alors 23 branches rectilignes.

Du point de vue de la plante, ces angles de divergence ne sont pas vraiment intéressants, car une bonne partie de la place disponible sur le capitule n’est pas exploitée. Ce problème survient à chaque fois que l’on choisit un angle de divergence rationnel, c’est-à-dire qui s’écrit comme le quotient de deux nombres entiers. Il est donc tentant de tester ce qui se passe lorsque l’angle de divergence n’est pas rationnel. On dit alors qu’il est irrationnel : on ne peut pas l’écrire comme le quotient de deux nombres entiers.

Un premier exemple de nombre irrationnel qui vient à l’esprit est celui du fameux nombre π, qui intervient dans le calcul du périmètre du cercle et dans tant d’autres formules mathématiques. La figure suivante montre le résultat obtenu si l’on choisit un angle de divergence égal à 1/π.

simulation pour 1/π.

Le nombre π est trop rationnel !

Curieusement, alors que π (donc aussi 1/π) n’est pas un nombre rationnel, la figure est du même type que celle obtenue pour un rationnel comme 11/23, avec ici 22 branches. Néanmoins ces branches sont ici légèrement courbées.

L’examen attentif de la figure donnée pour 1/π va nous permettre de mieux comprendre les qualités attendues de l’angle de divergence pour la plante. Commençons par observer ce qui se passe vers le centre : le processus commence par former 3 branches recourbées.

On peut expliquer facilement la présence de ces 3 branches : l’écriture décimale de π commence par 3,14159… donc dans une première approximation, π est proche de 3. Le nombre 1/π est donc proche de 1/3. Or, un angle de divergence 1/3 donnerait une figure à 3 branches rectilignes, et ce qui se passe vers le centre est donc une approximation de ce comportement.

Ces 3 branches sont ici courbées, car 1/π n’est pas exactement égal à 1/3. Puis, à mesure que les nouveaux fleurons sont formés, la distance au centre augmente, et approcher l’angle de divergence par 1/3 devient trop grossier. Les 3 branches centrales finissent alors par disparaître.

Comment expliquer ensuite la formation de 22 nouvelles branches ? Une autre approximation simple du nombre π, beaucoup plus précise que 3, est donnée par la fraction 22/7≃3,142857.

Ainsi l’angle de divergence est très bien approché par la fraction 7/22. S’il était égal à 7/22 on observerait 22 branches rectilignes. Comme l’approximation est très bonne mais pas exacte, on obtient ces 22 branches légèrement courbes.

Même si 1/π n’est pas un nombre rationnel, il est loin d’être optimal, car trop d’espace est perdu sur le capitule : sur la même surface, on pourrait mettre beaucoup plus de fleurons qui donneraient plus de graines ! La surface perdue vient du fait que l’angle de divergence 1/π est trop bien approché par des nombres rationnels. Pour que les fleurons soient disposés de manière très efficace sur le capitule, il faudrait donc utiliser un angle de divergence qui soit le plus mal possible approché par des nombres rationnels.

Le nombre d’or entre en scène

Le problème de l’approximation diophantienne (comment approcher un nombre quelconque par des nombres rationnels) est relié à la théorie des fractions continues, qui consiste à représenter tout nombre sous forme d’une fraction, éventuellement infinie lorsque le nombre est irrationnel. Par exemple, le nombre 1/π peut s’écrire sous la forme

écriture de l’inverse de π sous forme d’une fraction continue.

où la fraction se poursuit indéfiniment.

En tronquant cette fraction infinie, on obtient les meilleures approximations d’un nombre irrationnel donné par des rationnels : ce que l’on appelle les réduites. Par exemple, en arrêtant la fraction au nombre 7, on obtient la réduite 7/22 comme bonne approximation de 1/π.

approximation de l’inverse de π par l’une de ses réduites.

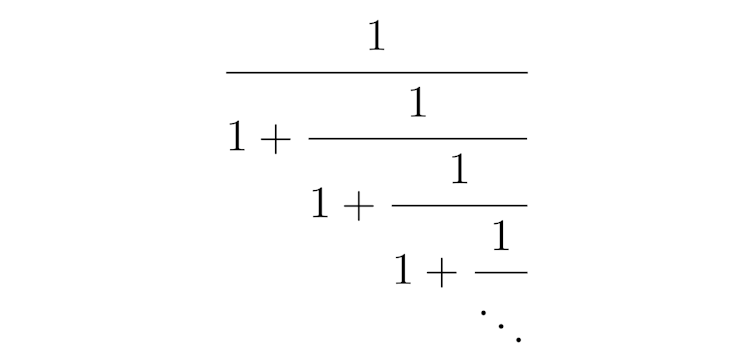
Toutefois il existe un nombre pour lequel ces réduites restent le plus éloignées possible : celui dont le développement en fraction continue ne comporte que des « 1 ». Il s’écrit

fraction continue pour l’inverse du nombre d’or.

Or ce nombre est précisément l’inverse du nombre d’or :

l’inverse du nombre d’or.

Cette théorie nous amène ainsi au choix optimum de l’angle de divergence, celui qui est le plus mal approché par des nombres rationnels : c’est l’angle dont le rapport avec un tour complet vaut l’inverse du nombre d’or, et que l’on nomme l’angle d’or. Voyons la figure donnée dans ce cas.

simulation lorsque l’angle de divergence vaut l’angle d’or 1/φ.

On observe effectivement avec l’angle d’or une bien meilleure utilisation de l’espace disponible : les fleurons sont disposés régulièrement sans laisser d’espace vide important sur le capitule. On note également une réelle ressemblance avec la disposition observée sur de vrais tournesols.

Et Fibonacci dans tout ça ?

Les spirales sur la figure de l’angle d’or correspondent aux « branches » que l’on observe dans les cas d’un angle de divergence (presque) rationnel : chaque réseau de spirales est associé à une approximation rationnelle de l’angle d’or par l’une de ses réduites. Comme dans les cas 1/6, 11/23 ou 1/π, le nombre de spirales (ou de branches) est donné par le dénominateur de la fraction définie par la réduite. Or les réduites de l’angle d’or ont pour dénominateurs successifs… les nombres de Fibonacci !

Ainsi la présence des nombres de Fibonacci dans les spirales des plantes est la signature du fascinant nombre d’or.

Sa difficulté particulière à être approché par des fractions lui a valu d’être sélectionné par l’évolution naturelle de nombreux végétaux. Il est remarquable de constater que des théories mathématiques a priori très éloignées de la botanique apportent un éclairage pertinent dans ce domaine.